企业营运根据上、下游关係，同时拥有客户与供应商两种的角色[如图一]，企业内部也会存在这两种关係的单位，譬如组装厂(内部客户)与射出成型厂(内部供应商)或组装厂(内部客户)与包材厂(内部供应商)等[如图二]，内部供应商必须满足内部客户的需求自是理所当然，然而，若组织运作不适当，往往会造成「内部供应商」的困扰。以下案例是某公司实际发生的情况。

[图一]

[图二]

　　T企业是一家集团公司，有多个分公司与事业部[如图三]，其中有一公司事业部，D事业部，所生产的产品并不对外销售，而是提供材料给各事业单位，形成所谓的内部供应商。D事业部虽然是内部供应商，同样的，也须背负营运上的品质、成本、交期等等的管理。

[图三]

　　由于D事业部的角色特殊，必须满足内部客户的生产需求，儘管各事业部都会共同参与月产销会议，也会提供週排程计画，但总有「计画赶不上变化」的无奈感，长期以往，插单、改单的情形演变成家常便饭，库存数也难以有效控制，成了D事业部资材单位的痛点。

　　幸好，T企业不仅有完善的企业资源规画系统(Enterprise Rresource Planning，ERP)，也有自行开发的製造执行系统(Manufacturing Execution System, MES)，两系统皆蒐集了庞大的数据，若能有效的利用这些数据，来预测各事业部的月产销计画量，并检视预测与事业部生管给的预估量之差异是否过大，从而提出问题，重新审视预估量。

　　我们挑选A、B、C一事业部来做预测。首先，我们从MES系统下载2016年1月到2017年12月某事业部的生产数据，如[图四]。

[图四]

　　从上图可知，2016年1月至2017年12月之间，该事业部的产量有逐月上升的趋势，但在2016年2月与2017年1月却突然往下降，原因是当月正好是农曆过年，工作日数较其它月份少，产量自然也较少。

　　然而，预测方式有很多类型，究竟要选择哪一类型的预测方式？由于是下载一段时间内的资料，因此，我们採用「时间序列」的方式来做预测，故我们使用不同「时间序列」的预测模型来预估。

　　移动平均法(Moving Average Method, MA)是定量需求预测方法中较简单的一种，它是利用过去数期的需求资料来建立预测值，其移动平均值是以特定的期数，如3个月、4个月或5个月等来计算，数学式如下

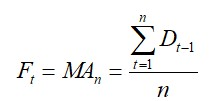
　　其中，Ft=第t期的预测值，Dt-1=第t-1期的需求量(实际值)，n=移动平均的期数。

　　对于本文所提出的数学式，实务上，我们不太可能用笔计算并比较。因此，我们利用EXCEL试算表来实现计算过程与结果，配合EXCEL试算表公式的呈现有助于理解数学式所代表的意义。故我们以EXCEL试算表计算上述数学式的预测值，如[表一]。

[表一]

　　我们举「2期预测」与「3期预测」说明EXCEL试算表的公式设定，余期，依此类推，如[表二]。

[表二]

　　用了这幺多的期数来预测，到底哪一期的预测方式比较好？我们可以用实际值与预测值之间的差距来定义「预测误差」(error)，计算式如下：

　　其中，et=第t期的预测误差，Dt=第t期的需求量(实际值)，Ft=第t期的预测值

　　RSFE表示累计误差(Running Sum of Forecast Error)

　　然而，仅是以这样的计算方式衡量预测误差，在正、负误差的影响下，会导致RSFE值的失準，因此，我们决定使用其它的方法来判断预测準确度。

　　MAE表示平均绝对误差(Mean Absolute Error)，其中n代表期数

 　　RMSE表示均方根误差(Root Mean Square Error)

　　MAPE表示平均绝对百分比误差(Mean Absolute Percent Error)

　　这三项评估指标的结果，数值愈小代表误差愈小，预测的结果愈準确。由于MAE与RMSE计算误差皆会有计算误差值大小取决于预测项目衡量值大小的问题，在某些情况下，预测值与实际值的误差比例远比预测误差的绝对数字更具参考价值，MAPE不仅仅考虑预测值与实际值的误差，还考虑了误差与实际值之间的比例。

　　学者Lewis(1982)认为，MAPE是最有效的评估指标，并将MAPE分为四种等级，如[表三]所示。

MAPE(%)	说    明
<10	高精準的预测
10-20	优良的预测
20-50	合理的预测
>50	不準确的预测

[表三]

　　因此，本篇案例将选用平均绝对百分比误差(MAPE)为主要的指标来衡量误差，以判断预测值的準确程度，同时辅以平均绝对误差(MAE)及均方根误差(RMSE)做为比较误差之準则，利用这些指标，找出较佳的预测模式。

　　我们选「2期预测」作为範例，以EXCEL试算表分别计算MAPE、RMSE与MAE值，如[表四]。

[表四]

同时说明EXCEL试算表的公式设定，余期，依此类推，如[表五]。

　　依照[表四]的方式，我们计算出各期MAPE、RMSE与MAE的误差值并彙整如下，如[表六]。从[表六]可以得知，在这个案例中，移动平均法的期数愈多，MAPE的误差愈大，以4个月期的MAPE，18.16%，误差最小，若以学者Lewis 区分的等级来说，属于优良的预测。

　　然而，这样就可以结束了吗？不，前面提到，2016年2月与2017年1月的产量突然往下降的原因是碰上农曆过年，因此，我们把这两个月的资料另外处理，再重新计算各期的MAPE、RMSE与MAE，看看会发生什幺情况，如[表七]。

期数	MAPE	RMSE	MAE
2个月期	17.97%	19693.9	13691.1
3个月期	18.37%	18817.5	14347.0
4个月期	18.16%	17944.7	14560.2
5个月期	18.37%	18143.3	15346.1
6个月期	19.03%	19468.0	16547.3
12个月期	25.14%	25780.9	24273.8

[表六]

期数	MAPE	RMSE	MAE
2个月期	10.67%	12673.1	10494.3
3个月期	10.35%	11812.8	10332.8
4个月期	10.22%	11708.8	10356.5
5个月期	11.06%	13376.6	11493.5
6个月期	12.42%	15239.9	13108.7
11个月期	19.54%	22771.9	21098.1

[表七]

　　我们发现，这样处理后，各期的MAPE、RMSE与MAE值明显变小了，4个月期的MAPE依然是误差最小，10.22%，可见得这两个月的数据足以影响整个预测模型的结果，因此，后续的预测模型将不包含这两个月的资料。绘製误差最小MAPE之4期预测值与实际量，如[图五]所示。

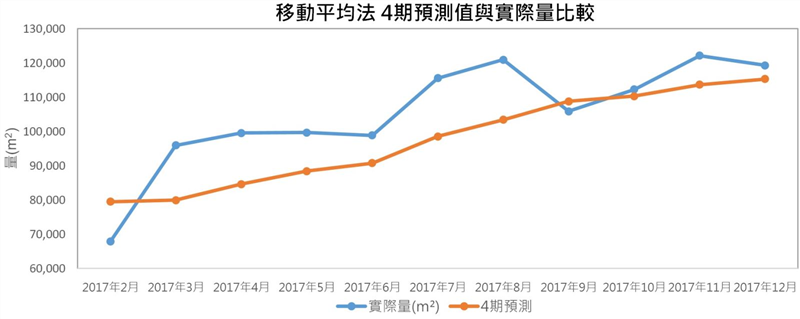
[图五]

　　移动平均法的优点在于容易计算与了解，缺点是每一期权重都相同，若在序列中有变动发生，则移动平均预期的反应会很迟缓。若我们想藉由调整移动平均法使其更準确的反映资料中的波动情况，则可给予近期资料较高的权重，此种方法称为加权移动平均法(Weighted Moving Average, WMA)，其数学式如下：

　　其中，F_t=第t期的预测值，W_t-1=第t-1期的权重值，D_t-1=第t-1期的需求量(实际值)，n=移动平均的期数。

　　权重的选择，最常用的方式是经验法和试误法，但是我们可以设定不同组的权重，然后透过试预测进行比较分析，选择预测误差小者作为最终的权重。我们以5个月期及其一组权重值作为範例，以EXCEL试算表计算预测值，如[表八]。

[表八]

　　同时说明EXCEL试算表的公式设定，余期，依此类推，如[表九]。

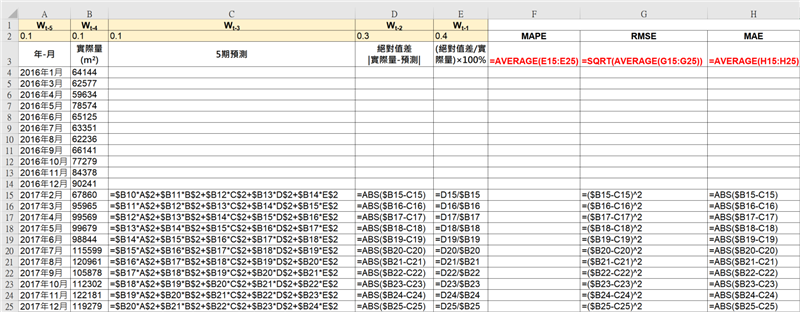
[表九]

　　最后，我们将各期数与不同权重的预测误差彙整为一张表，如[表十]。

[表十]

　　从[表十]的MAPE值可以得知，当计算週期为3个月期，权重值为0.2、0.2及0.6的加权移动平均法，可以有最低的MAPE值，故预测2017年2月到2017年12月的生产量时，以此为準。绘製3期(W_i=0.2、0.2与0.6)预测值与实际量，如[图六]所示。

[图六]

　　当移动平均间隔中出现趋势时，给近期实际值赋予较大的权重，给远期实际值赋予较小的权重，进行加权移动平均，预测效果较好。但要为各时期分配权重并找出合适的权重值是一件非常耗时的事。为能经济有效的处理，并提供良好的短期预测，「指数平滑法」是不错的选择，其数学式如下：

　　其中，F_t=第t期的预测值，F_t-1=第t-1期预测值，D_t-1=第t-1期的需求量(实际值)，α为平滑係数(0<α<1)。α→0，表示预测误差的调节能力小(平滑度高，愈相信预测值)；α→1，表示预测误差的调节能力大(敏感度高，愈相信实际值)

　　在计算的过程中我们会发现，上式需要有期初预测值，一般可以选取上一期的实际值、移动平均法求得或前几期观测值的平均值作为初始值。

　　我们以α=0.6作为範例，初始值设为预测期之前三期的平均值，以EXCEL试算表计算预测值，如[表十一]。

[表十一]

　　同时说明EXCEL试算表的公式设定，余期，依此类推，如[表十二]。

[表十二]

　　最后，我们将不同α值的预测误差彙整为一张表，如[表十三]。

α	MAPE	RMSE	MAE
0.1	17.41%	19346.9	18356.0
0.2	14.05%	15623.4	14494.3
0.3	12.00%	13648.3	12123.6
0.4	11.21%	12669.1	11153.6
0.5	10.72%	12260.6	10545.6
0.6	10.42%	12190.5	10159.0
0.7	10.24%	12330.8	9905.5
0.71	10.22%	12353.3	9885.0
0.8	10.33%	12609.8	9955.3
0.9	10.47%	12987.8	10062.6

[表十三]

　　从[表十三]得知，当指数平滑法的α值设为0.7时，可以使2017年2月到2017年12月的预测与实际量有较好的MAPE值10.24%，再进一步分析发现，α值设为0.71时，有最低的MAPE值10.22%。而其预测值与实际量的比较，如[图七]所示。

[图七]

　　上述的指数平滑法适合用在数据比较平稳，没有较大的波动时，也称为一次指数平滑法，如果数据具有某种趋势，但无季节变动，则二次指数平滑法是较为实用的方法。从[图四]可以知道，该事业部的生产量有逐月上升的趋势且无季节变动，因此，我们採用 Robert G. Brown 单一参数线性指数平滑法来解决这一问题，其数学式如下：

式中，T为预测的期数

又

且

式中，为一次指数平滑值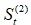，为二次指数平滑值，D_t=第t期的需求量(实际值)，α是平滑係数(0<α<1)。

当t=1时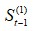， 与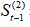都是没有数据的，需事先给定，通常採用 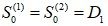或序列最初几期数据的平均值。在这个案例中，我们以α=0.3作为範例，初始值我们採用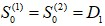，以EXCEL试算表计算预测值，如[表十四]。

[表十四]

同时说明EXCEL试算表的公式设定，余期，依此类推，如[表十五]

[表十五]

　　最后，我们将不同α值的预测误差彙整为一张表，如[表十六]。

α	MAPE	RMSE	MAE
0.1	13.37%	15844.5	14015.6
0.2	9.35%	10687.2	9199.8
0.21	9.27%	10614.5	9084.6
0.3	9.57%	11003.4	9119.4
0.4	10.34%	12191.9	9699.1
0.5	11.13%	13561.8	10362.1
0.6	12.23%	15011.7	11453.8
0.7	13.67%	16550.2	12967.0
0.8	15.43%	18220.2	14833.4
0.9	16.96%	20088.8	16449.5

[表十六]

　　从[表十六]得知，当二次指数平滑法的α值设为0.2时，可以使2017年2月到2017年12月的预测与实际量有较好的MAPE值9.35%，再进一步分析发现，α值设为0.21时，有最低的MAPE值9.27%，以学者Lewis 区分的等级来说，属于高精準的预测(MAPE<10%)。而其预测值与实际量的比较，如[图七]所示。

[图七]

　　迴归分析(Regression analysis)除了可以用来观察两个或两个以上的变数之间的因果关係外，还可以被用来作为时间序列的预测工具。我们以时间(t)为自变数，生产量(y_t)为应变数，随着时间的变动来预测生产的需求量，由于该事业部的生产量有逐月上升的趋势，如[图四]，因此，我们可利用最小平方法(Method of least squares)求得线性迴归模型(Linear regression model)：

其中，

　　式中，y_i=第t期的预测值，a:在t=0时的y_i值，b表示直线斜率，n为期数。

　　我们以EXCEL试算表先用2016年的资料(不含2月份)求得初始的迴归方程式，如[图八]，再用此迴归方程式求得次月(即2017年2月)的需求预测，如[表十七]。

[注:迴归方程式 x以t替代；EXCEL试算表可以设定显示公式]

[图八]

No.	年-月	实际量(m2)	预测	迴归方程式	绝对值差 |实际量-预测|	(绝对值差/实际量)×100%
12	2017年2月		83,582	y=2,207.9t+57,087

[表十七]

将2017年2月份的实际量填入后，求得绝对值差、(绝对值差/实际量)×100%。再利用2016年 (不含2月份)到2017年2月份，12笔实际生产量的数据以迴归分析法预测2017年3月的生产量，如[表十八]。

No.	年-月	实际量(m2)	预测	迴归方程式	绝对值差 |实际量-预测|	(绝对值差/实际量)×100%
12	2017年2月	67,860	83,582	y=2,207.9t+57,087	15,722	23.2%
13	2017年3月		80,550	y=1,603.2t+59,708

[表十八]

依此方式，由EXCEL试算表完成至2017年12月份的资料，如[表十九]。

No.	年-月	实际量(m2)	预测	迴归方程式	绝对值差 |实际量-预测|	(绝对值差/实际量)×100%
12	2017年2月	67,860	83,582	y=2,207.9t+57,087	15,722	23.2%
13	2017年3月	95,965	80,550	y=1,603.2t+59,708	15,415	16.1%
14	2017年4月	99.569	86,896	y=2,111.4t+57,336	12,673	12.7%
15	2017年5月	99,679	92,629	y=2,473.5t+55,526	7,051	7.1%
16	2017年6月	98,844	96,982	y=2,649.8t+54,585	1,862	1.9%
17	2017年7月	115,599	100,098	y=2,690.9t+54,353	15,501	13.4%
18	2017年8月	120,961	106,435	y=2,994.8t+52,529	14,526	12.0%
19	2017年9月	105,878	112,657	y=3,249.6t+50,915	6,779	6.4%
20	2017年10月	112,302	114,481	y=3,142.6t+51,629	2,179	1.9%
21	2017年11月	122,181	117,188	y=3,111.5t+51,846	4,994	4.1%
22	2017年12月	119,279	121,250	y=3,176.3t+51,371	1,971	1.7%

[表十九]

　　最后，我们计算2017年2月到2017年12月的MAPE、RMSE、MAE值分别为9.10%、10571.8及8970.2，其预测值与实际量的比较，如[图九]所示。

[图九]

 

　　本案例使用了移动平均法、加权移动平均法、指数平滑法与线性迴归模型四种预测方法之52种模型来预测未来需求量，其预测模型整理如下：

1. 移动平均法

以特定期数2个月期、3个月期、4个月期、5个月期、6个月期、12个月期，共6种模型。

2. 加权移动平均法

以2个月期加权权数4种组合、3期加权权数8种组合、4期加权权数7种组合、5期加权权数6种组合，共25种模型。

3. 指数平滑法

一次指数平滑法，平滑指数α值0.1至0.9，共10种模型。

二次指数平滑法，平滑指数α值0.1至0.9，共10种模型。

4. 线性迴归模型

线性迴归预测方式1种模型。

分别将四种预测方法较佳的模型与条件整理如下，如[表二十]：

预测方法	条件	MAPE	RMSE	MAE
移动平均法	4个月期	10.22%	11708.8	10356.5
加权移动平均法	3个月期，权重值为0.2、0.2及0.6	10.04%	11751.3	9791.9
指数平滑法	α=0.21	9.27%	10614.5	9084.6
线性迴归模型		9.10%	10571.8	8970.2

[表二十]

　　因此，本案例採用线性迴归模型做为次月的预测模型，同时，比较生管排程的计画量与预测量，结果发现以预测的方法比生管计画有较少的误差，如[表二十一]，此预测方法已导入该事业部，可以有效减少生管插单、改单与库存的情形。

[表二十一]

　　前文提到，过年当月的工作天数远远少于其它月份，着实影响整个预测模型，因此必须另外处理，处理的方式可以使用其它方法建立模型，但由于本案例的过年月份数据少，不足以建立模型，因此暂时予以忽略。

　　本文虽然使用内部客户生产量来预测，亦可使用自己出给内部客户的出货量来预测，实务上，我们对于外部顾客的生产量是无法得知，但可以运用本身出给该客户的数量来预测。

总结：

　　预测方法的种类非常多，究竟要选用哪一种方式？最佳的预测方法也不一定是準确度最高或是成本最低，而是取决于管理者对预测的準确度与成本的需求。

　　就本例而言，四种预测方法都比生管计画要来得準确许多，最后採取迴归分析法来预测次月，因为它的模型误差最小，但不代表每个月都是以迴归模型来预测，而是以这四种模型中哪一个月的预测误差最小，当作是次月的预测模型，一旦预测误差愈来愈大时，参考[表三]，代表预测模型已不适用，必须另觅他法。

　　预测分析的目的在于后续的管理策略为何？本文的案例，主要是要解决内部客户预估失準所造成的库存增加；因库存问题可能造成的品质隐患；插单、改单与追加订单造成的成本增加，如加班、人力调度、物料需求调整等等。根据预测数据，生管可以评估后续的管理策略，以提供上一阶主管做管理决策。如[图十]所示。

[图十]

 

除此之外，生管可以依据预测数据来检视内部客户提供的预估是否超过预测自设的比例，一旦超出，便须更进一步地向内部客户确认预估的可靠性，从而减少计画排程的变异，进而减少不必要的成本与浪费，解决这些问题该事业部生管导入预测的主要目的。

儘管预测模型的选用是重要的事，更重要的是，就算模型预测得非常準确，若没有採取任何的管理策略，「预测」这件事情也就没有多大的意义。

 

参考资料：

1. 陈宽茂(2004)。CPFR流程下之订单预测方法。国立政治大学资讯管理研究所硕士論文。
2. 杨明德(2012)。销售预测之研究-以T公司花莲营业处为例。国立东华大学管理学院高阶经营管理硕士在职专班論文。
3. 网站: https://www.itsfun.com.tw/指数平滑法/wiki-8336915
4. 指数平滑法中平滑系数的选择研究https://wenku.baidu.com/view/508b1caff121dd36a32d82c5.html